Các thuật toán sắp xếp cơ bản: Đâu là sự lựa chọn tốt nhất?

Hiểu về các thuật toán sắp xếp giúp bạn tổ chức dữ liệu một cách có hệ thống, từ đó dễ dàng tìm kiếm, truy cập và phân tích. Trong bài viết này, cùng mình tìm hiểu về các thuật toán sắp xếp cơ bản và cách triển khai chúng bằng TypeScript.

1. Bubble Sort (Sắp Xếp Nổi Bọt)

Thuật toán Bubble Sort là một trong những thuật toán sắp xếp đơn giản nhất. Ý tưởng chính là duyệt qua danh sách cần sắp xếp liên tục, so sánh từng cặp phần tử liền kề và hoán đổi chúng nếu ở sai thứ tự.

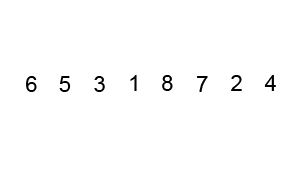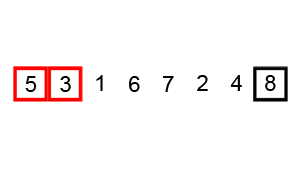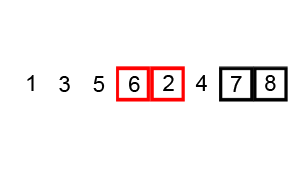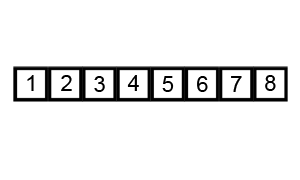
Bắt đầu từ đầu danh sách, so sánh hai phần tử đầu tiên.
Nếu phần tử thứ nhất lớn hơn phần tử thứ hai, hoán đổi chúng.
Tiếp tục với cặp phần tử tiếp theo cho đến cuối danh sách.
Lặp lại quá trình trên cho đến khi không có sự hoán đổi nào xảy ra trong một lần duyệt.

function bubbleSort(arr: number[]): number[] {
  let n = arr.length;
  for (let i = 0; i < n - 1; i++) {
    
    let swapped = false;
    for (let j = 0; j < n - i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
        swapped = true;
      }
    }

    if (!swapped) break;
  }
  return arr;
}

console.log(bubbleSort([5,3,4,12,2])) //LOG: [2, 3, 4, 5, 12]

Vòng for ngoài: chạy n – 1 lần, với n là độ dài của mảng.
Vòng for trong: so sánh và hoán đổi các cặp phần tử liền kề.
Biến swapped: giúp tối ưu hóa thuật toán bằng cách dừng sớm nếu mảng đã được sắp xếp.

2. Selection Sort (Sắp xếp chọn)

Thuật toán sắp xếp Selection Sort hoạt động bằng cách liên tục tìm phần tử nhỏ nhất (hoặc lớn nhất) trong danh sách chưa được sắp xếp và đưa nó về vị trí đúng trong danh sách.

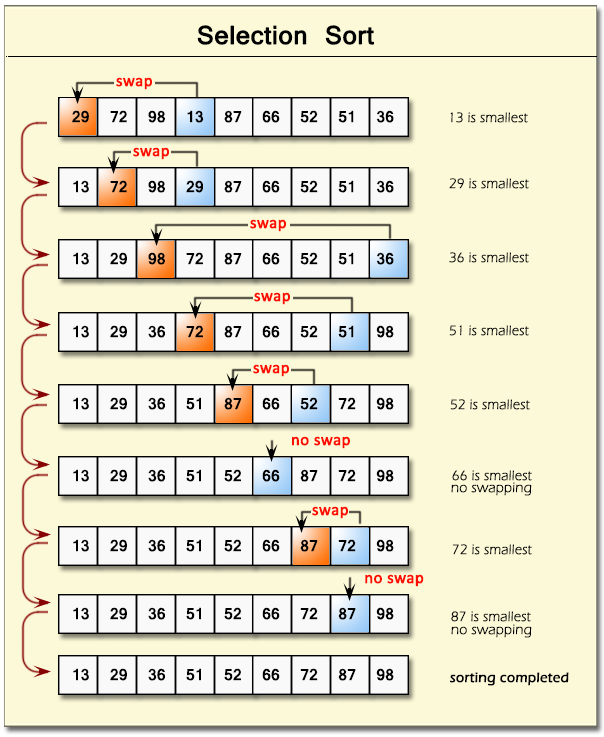
Duyệt qua toàn bộ mảng để tìm phần tử nhỏ nhất.
Hoán đổi phần tử nhỏ nhất với phần tử đầu tiên của mảng.
Tiếp tục với phần còn lại của mảng (bỏ qua phần tử đầu tiên đã được sắp xếp).

function selectionSort(arr: number[]): number[] {
  let n = arr.length;
  for (let i = 0; i < n; i++) {

    let minIndex = i;
    for (let j = i + 1; j < n; j++) {
      if (arr[j] < arr[minIndex]) {
        minIndex = j;
      }
    }

    [arr[i], arr[minIndex]] = [arr[minIndex], arr[i]];
  }
  return arr;
}

console.log(selectionSort([12, 5, 4, 32, 2])) // LOG: [2, 4, 5, 12, 32]

Vòng for ngoài: duyệt qua từng phần tử trong mảng.
Vòng for trong: tìm phần tử nhỏ nhất trong phần còn lại của mảng.
Hoán đổi vị trí: đưa phần tử nhỏ nhất về vị trí hiện tại.

3. Insertion Sort (Sắp Xếp Chèn)

Thuật toán Insertion Sort xây dựng danh sách đã sắp xếp từng phần tử một. Nó lấy mỗi phần tử và chèn vào vị trí thích hợp trong danh sách đã sắp xếp trước đó.

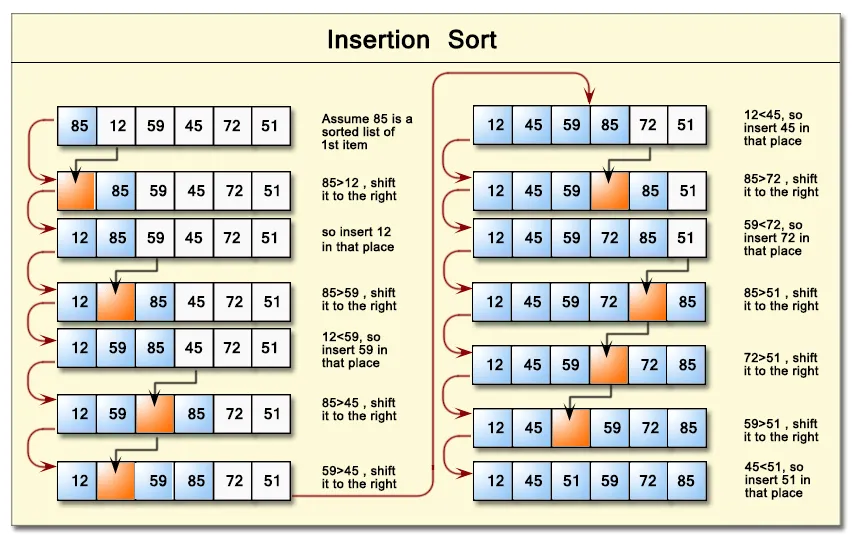
Bắt đầu từ phần tử thứ hai trong mảng.
So sánh phần tử hiện tại với các phần tử trước đó.
Di chuyển các phần tử nhỏ hơn lên một vị trí để tạo chỗ trống.
Chèn phần tử hiện tại vào vị trí thích hợp.

function insertionSort(arr: number[]): number[] {
  let n = arr.length;
  for (let i = 1; i < n; i++) {
    let key = arr[i];
    let j = i - 1;

    while (j >= 0 && arr[j] > key) {
      arr[j + 1] = arr[j];
      j--;
    }

    arr[j + 1] = key;
  }
  return arr;
}

console.log(insertionSort([10, 4, 63, 9, 12])) //LOG: [4, 9, 10, 12, 63]

Biến key: lưu trữ giá trị của phần tử hiện tại cần chèn.
Vòng lặp while: di chuyển các phần tử lớn hơn key lên một vị trí.
Chèn key: đặt key vào vị trí trống thích hợp.

4. Quick Sort (Sắp Xếp Nhanh)

Quick Sort là thuật toán sắp xếp hiệu quả, sử dụng phương pháp chia để trị, chọn một pivot và phân chia mảng thành hai phần dựa trên pivot.

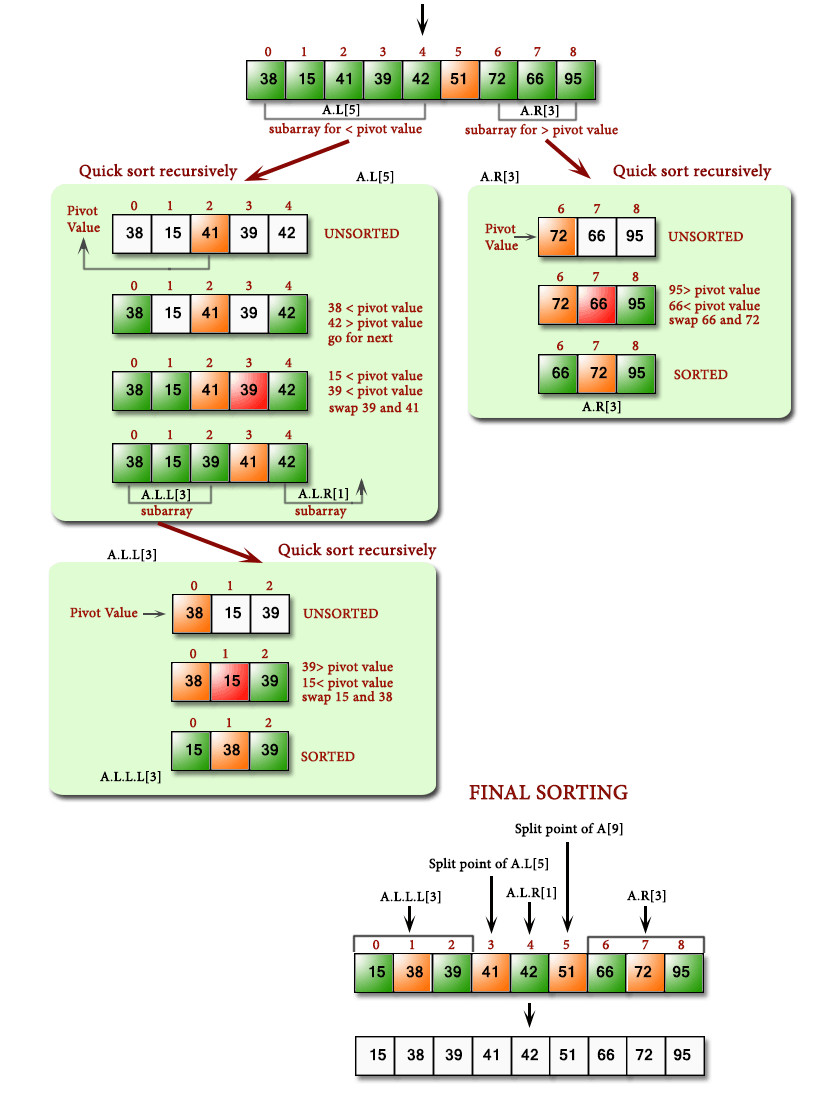
Chọn một phần tử làm pivot – thường sẽ lấy giữa.
Phân chia mảng thành hai phần: phần nhỏ hơn pivot và phần lớn hơn pivot.
Đệ quy áp dụng thuật toán cho hai phần này.

function quickSort(arr: number[]): number[] {
  if (arr.length <= 1) return arr;
  let pivot = arr[arr.length - 1];
  let left: number[] = [];
  let right: number[] = [];
  for (let i = 0; i < arr.length - 1; i++) {
    if (arr[i] < pivot) left.push(arr[i]);
    else right.push(arr[i]);
  }
  return [...quickSort(left), pivot, ...quickSort(right)];
}

console.log(quickSort([1,4,6,9,8])) //LOG: [1, 4, 6, 8, 9]

Chọn pivot: phần tử cuối cùng của mảng.

Phân chia mảng:

left: Chứa các phần tử nhỏ hơn pivot.
right: Chứa các phần tử lớn hơn hoặc bằng pivot.

Đệ quy: Áp dụng quickSort cho left và right.

5. Merge Sort (Sắp Xếp Trộn)

Merge Sort là thuật toán sắp xếp ổn định, cũng sử dụng phương pháp chia để trị. Nó chia mảng thành hai nửa, sắp xếp từng nửa và sau đó trộn chúng lại.

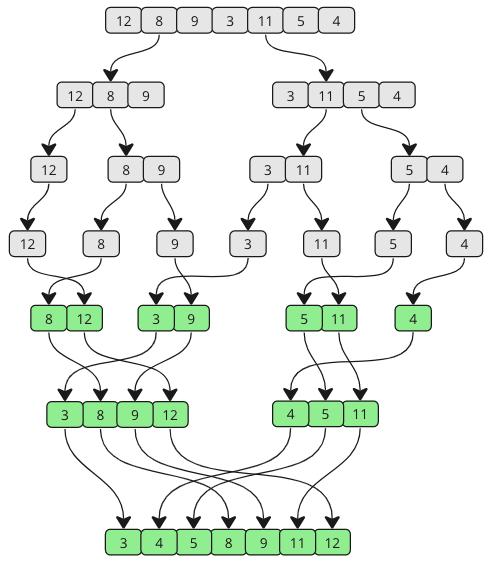
Chia mảng thành hai nửa cho đến khi mỗi phần chỉ còn một phần tử.
Trộn hai mảng con đã được sắp xếp thành một mảng duy nhất.

function mergeSort(arr: number[]): number[] {
  if (arr.length <= 1) return arr;
  let mid = Math.floor(arr.length / 2);
  let left = mergeSort(arr.slice(0, mid));
  let right = mergeSort(arr.slice(mid));
  return merge(left, right);
}

function merge(left: number[], right: number[]): number[] {
  let result: number[] = [];
  let i = 0, j = 0;
  while (i < left.length && j < right.length) {
    if (left[i] < right[j]) {
      result.push(left[i]);
      i++;
    } else {
      result.push(right[j]);
      j++;
    }
  }

  return result.concat(left.slice(i)).concat(right.slice(j));
}

console.log(mergeSort([9,5,3,8,5,3])) //LOG: [3, 3, 5, 5, 8, 9]

Chia mảng: sử dụng slice để chia mảng thành left và right.

Đệ quy: gọi mergeSort cho left và right.

Hàm merge:

So sánh phần tử đầu tiên của left và right.
Thêm phần tử nhỏ hơn vào result.
Tiếp tục cho đến khi một trong hai mảng hết phần tử.
Nối các phần tử còn lại vào result.

6. Độ phức tạp của các Thuật toán

Bên dưới mình có để một hình ảnh về độ phức tạp của các thuật toán. Bạn hãy lưu ý rằng ký hiệu Big(O) trong hình thể hiện độ phức tạp tối thiểu mà các thuật toán này có thể đạt được trong trường hợp tốt nhất hoặc trung bình.

Lý do mình khuyên các bạn nên xem và ghi nhớ những thông tin này là vì một số nơi phỏng vấn có thể sẽ hỏi về nó. Ngoài ra, hiểu rõ về độ phức tạp của thuật toán sẽ giúp bạn lựa chọn giải pháp phù hợp hơn khi viết code.

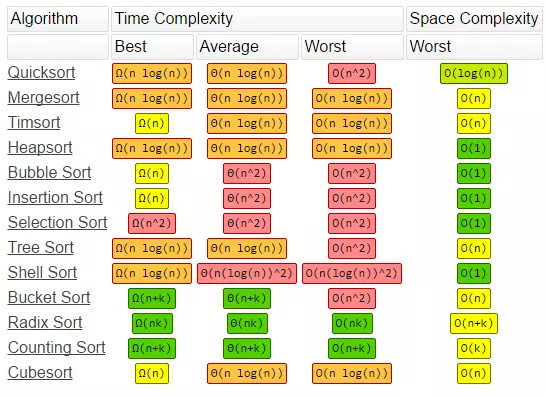
Bubble Sort, Selection Sort, Insertion Sort: thích hợp cho mảng nhỏ ít giá trị hoặc đơn giản là cần một thuật toán dễ hiểu và áp dụng. Time Complexity trong trường hợp Tồi tệ nhất (Worst) của cả ba thuật toán đều là O(n²), vì vậy chúng không hiệu quả khi làm việc với các tập dữ liệu lớn.
Quick Sort: Lựa chọn tốt cho mảng lớn, nhưng cần cẩn thận cân nhắc với trường hợp tệ nhất. Đây là một thuật toán với độ phức tạp trung bình là O(n log n).
Merge Sort: Là thuật toán sắp xếp ổn định và đảm bảo hiệu suất với độ phức tạp O(n log n) trong mọi trường hợp. Merge Sort thường được lựa chọn khi cần đảm bảo tính ổn định và hiệu suất tốt cho tập dữ liệu lớn.

7. Kết luận

Hiểu rõ các thuật toán sắp xếp cơ bản là một bước quan trọng khi bắt đầu hành trình trở thành developer. Dù có những thuật toán sắp xếp phức tạp hơn, nhưng các thuật toán cơ bản này sẽ giúp bạn xây dựng nền tảng vững chắc.

Một vài lời khuyên cho bạn:

Thực hành: hãy tự triển khai các thuật toán này và thử nghiệm với nhiều bộ dữ liệu khác nhau.
Hiểu rõ về độ phức tạp: nắm vững khái niệm về độ phức tạp thời gian và không gian để lựa chọn thuật toán phù hợp.
Sau khi nắm vững các thuật toán cơ bản, hãy khám phá các thuật toán sắp xếp nâng cao như là Heap Sort, Radix Sort,…